B. Reproducibility:

Next: C. Speed: Up: Desired Properties of Random Previous: A. Randomness:

B. Reproducibility:

In the early days of computers, it was suggested that one could make a special circuit element which would deliver truly random numbers. Computer vendors have not supplied such an element because it is not trivial to design a device to deliver high quality numbers at a sufficient rate. Even more importantly, debugging codes would becomes much more difficult if each time the code was run a completely irreproducible sequence were to be generated. In Monte Carlo simulations, bugs may be manifest only at certain times, depending on the sequence of random numbers obtained. In order to detect the errors, it is necessary to repeat the calculations to find out how the errors occurred. The feature of reproducibility is also helpful while porting the program to a different machine. If we have a sample run from one machine available, then we can try an identical run on a different machine and verify that it ported correctly. Such reproducible random number generators are said to be pseudo random (PRNG), and we shall call the numbers produced by such generators as PRNs.

There is a conflict between the requirements of reproducibility and randomness. On a finite memory computer, at any step k in the sequence the PRNG has an internal state specifiable conceptually by an integer , where the size of this integer is not necessarily related to the word length of the computer. For each state S in the sequence, there is a mapping that gives a random number the user sees, . We also have an iteration process to determine the next state of the sequence from the current state, . All PRNGs can be classified by the internal state space, the mapping, and the iteration. The sequence is defined once we have specified the initial starting state known as the seed. Fig. illustrates the procedure for obtaining pseudo-random sequences described above.

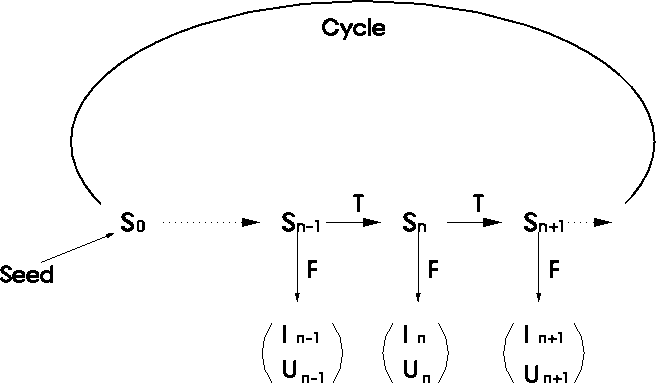
Figure: A pseudo-random sequence is defined by the internal state space, the mapping, the iteration, and the initial state.

Now let us return to the possible conflict between the properties of reproducibility and randomness: if it is reproducible then it cannot be perfectly random since knowing the sequence will make betting on the next number easy. How do we resolve the incompatibility between the two properties? In common sense terms, we mean a good PRNG is one whose numbers are uncorrelated as long as you do not explicitly try to back out the mapping and iteration processes and use that to predict another member of the sequence. PRNG's have not been designed to be good cryptographic sequences.

Next: C. Speed: Up: Desired Properties of Random Previous: A. Randomness:

The National Center for Supercomputing Applications
University of Illinois at Urbana-Champaign

ashoks@ncsa.uiuc.edu

B. Reproducibility:

Last modified: September 16, 1997